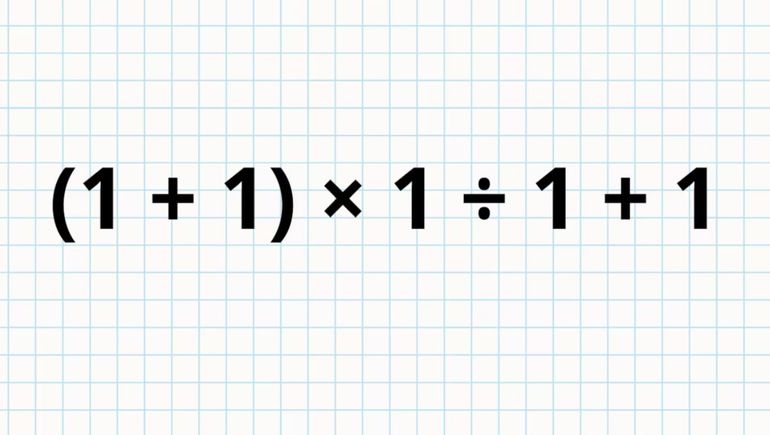Esta cuenta matemática parece fácil pero no lo es: ¿Podés resolverla?

A primera vista, la cuenta (1 + 1) × 1 ÷ 1 + 1 parece trivial. Muchos pueden resolverla casi automáticamente, pero la sorpresa aparece cuando se ignora la jerarquía de las operaciones. Esta cuenta se convierte en un excelente ejemplo de cómo el orden en que se realizan las operaciones matemáticas puede alterar el resultado final.

Más allá de sumas y multiplicaciones, este tipo de ejercicios exige concentración y memoria de reglas básicas de cálculo.

Para resolver correctamente la cuenta, es necesario recordar la jerarquía que regula las matemáticas: primero paréntesis, luego multiplicaciones y divisiones, y por último sumas y restas.

Esta es la lógica que hay que seguir:

• Paréntesis: (1 + 1) = 2

• Multiplicación: 2 × 1 = 2

• División: 2 ÷ 1 = 2

• Suma final: 2 + 1 = 3

Si alguien ignorara esta secuencia y resolviera la operación de izquierda a derecha sin aplicar correctamente las reglas, el resultado sería incorrecto. Esta simple diferencia resalta cómo un error de procedimiento puede llevar a confusión, incluso con operaciones básicas.

Más ejemplos para ejercitar la mente

matematicas.jpg

Resolver la cuenta (1 + 1) × 1 ÷ 1 + 1 paso a paso demuestra la importancia de respetar la jerarquía de operaciones matemáticas.

Este tipo de problemas se multiplica en distintas formas. Por ejemplo:

• (2 + 3) × 2 ÷ 5 + 1

  Resuelto correctamente, se obtiene: (2 + 3) = 5 → 5 × 2 = 10 → 10 ÷ 5 = 2 → 2 + 1 = 3.

• 4 + 6 ÷ (1 + 2) × 3

  Primero los paréntesis: (1 + 2) = 3 → división: 6 ÷ 3 = 2 → multiplicación: 2 × 3 = 6 → suma: 4 + 6 = 10.

• (5 × 2 + 3) ÷ 4

  Paréntesis primero: 5 × 2 = 10 → 10 + 3 = 13 → división: 13 ÷ 4 = 3,25.

• (3 + 7) ÷ 2 × (1 + 1)

  Paréntesis: (3 + 7) = 10 y (1 + 1) = 2 → división: 10 ÷ 2 = 5 → multiplicación: 5 × 2 = 10.

• 8 ÷ 2 × (2 + 2)

  Paréntesis: (2 + 2) = 4 → división y multiplicación de izquierda a derecha: 8 ÷ 2 = 4 → 4 × 4 = 16.

Estos ejercicios muestran que la combinación de operaciones puede transformar un cálculo simple en un reto mental que exige atención. Incluso pequeñas modificaciones en la estructura de la cuenta producen resultados diferentes, lo que obliga a revisar cada paso cuidadosamente.

Por qué prestar atención al detalle

Aunque muchos estudiantes aprenden estas reglas desde la escuela primaria, los errores surgen cuando se intenta resolver de memoria sin escribir cada paso. Operaciones aparentemente simples pueden generar dudas o confusiones. Además, este tipo de cuentas sirve como entrenamiento cognitivo, mejorando la concentración y la capacidad de razonamiento lógico.

En matemáticas, cada símbolo tiene su peso. La multiplicación no se iguala a la suma, y los paréntesis cambian la prioridad de las operaciones. Practicar con ejemplos como (1 + 1) × 1 ÷ 1 + 1 permite reforzar la memoria operativa y reduce errores en cálculos de matemática más complejos. Desde cuentas básicas hasta operaciones algebraicas, respetar la jerarquía garantiza resultados precisos y confiables.

Para quienes buscan desafiarse más, incluso se pueden crear ejercicios con tres o más operaciones distintas y paréntesis anidados, como (2 + 3 × (1 + 2)) ÷ 5 + 1, donde la atención al detalle se vuelve imprescindible.